Molecular Geometry¶
Info
Although entirely described by a 2D formula, a molecule exists as a 3D entity. The exact molecular geometry is defined by torsion angles, the concept of whom is presented and illustrated.
Number of Pages: 25 (±0 hours read)
Last Modified: May 2006
Prerequisites: None
2D/3D¶
Molecules Considered as 2D Structures¶
The way molecules have been perceived and defined has changed over the years. In the early 1970s, medicinal chemists considered molecules as mere topological two-dimensional (2D) entities with associated chemical and physicochemical properties.
articles
An Electrotopological-State Index for Atoms in Molecule Kier LB and Hall LH Pharm. Res. 7 1990
Decomposition of the Wiener Topological Index. Application to Drug-Receptor Interactions Lukovitz I J. Chem. Soc. Perkin Trans II. 1667-71 1988
Predicting Chemistry from Topology Rouvray DH Scientific American Sep. 255 1986
The Three-Dimensional Shape of a Molecule¶
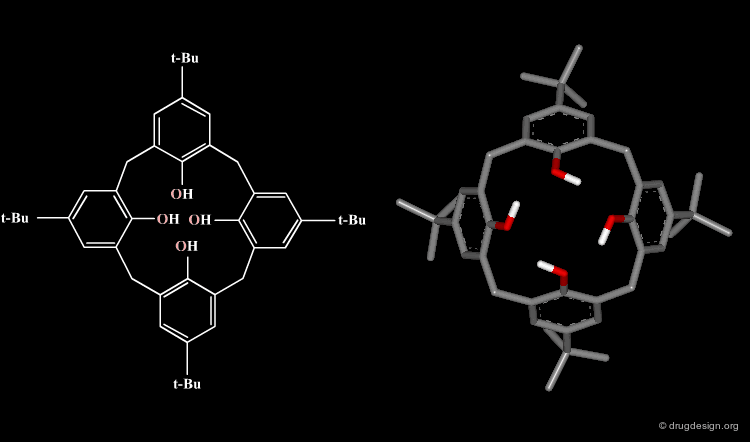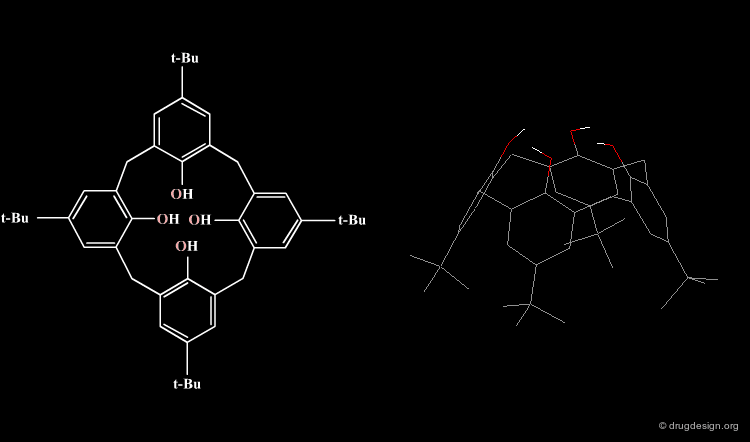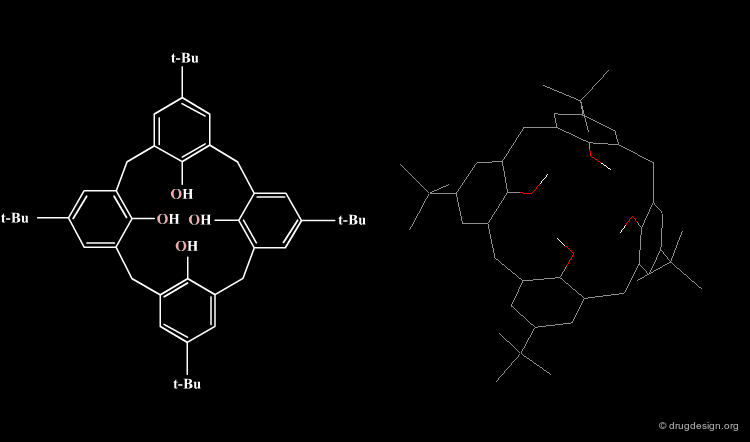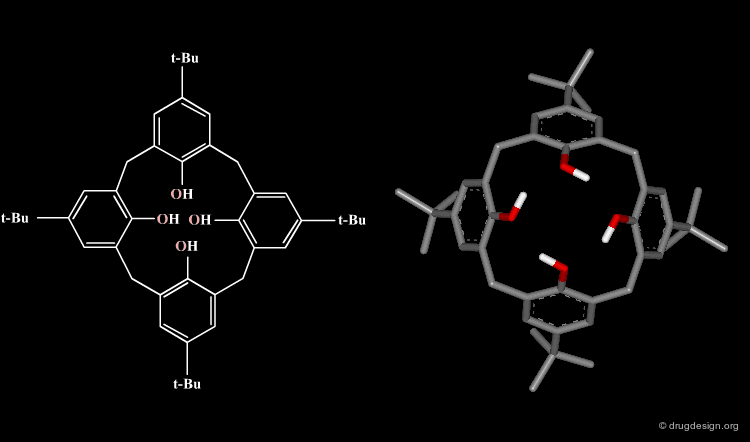
The formula of a molecule can be drawn in two-dimensions as on a piece of paper; however it really exists in three-dimensional space with precise geometrical features. For example the calix[4]arene illustrated here has a cone-like structure, a geometry that is not carried by its 2D formula.
articles
Synthesis of Calix[4]arene Triflates and Their Unusual chemical Reactivity in Palladium-Catalyzed Reactions Chowdhury S, Bridson JN and Georghiou PE J. Org. Chem. 65(11) 2000
Calixarenes. 20. The Interaction of Calixarenes and Amines Gutsche CD, Iqbal M and Alam I J. Am. Chem. Soc. 109 1987
book
Vicens J and Bohmer V Calixarenes, a Versatile Class of Macrocyclic Compounds Academic Press 1991
2D and 3D Representations¶
There is no obvious relationship between the 2D and the 3D structure of a molecule. The 3D geometries are of great importance because they represent the very molecular determinants that control molecular interactions. They are essential to understanding and influencing biological processes and their possible aberrations. This will be illustrated in many chapters of this course.
articles
Rapid Conversion of Molecular Graphs to Three-Dimensional Representation Using the MOLGEO Program Gordeeva EV, Katritzky AR, Shcherbukhin VV and Zefirov NS J Chem. Inf. Comput. Sci. 33 1993
book
Mekenyan O and Bonchev D FECS 3rd International Conference on Chemistry and Biotechnology of Biologically Active Natural Products, Vol 3, Plenary Lectures: Bioorganic Chemistry and Structural Elucidation and Chemical Transformation of Natural Products VCH Publishers 1987
A Molecule: An Assembly of Atoms in 3D¶
A molecule is an assembly of atoms in 3D. The 2D structure defines the atoms and the connections between them; it becomes 3D when the location of the atoms is considered. The following molecule consists of 63 atoms, 66 bonds and 4 rings.
articles
Molecular Connectivity III: Relationship to Partition Coefficient Murray WJ, Hall LH, and Kier LB J. Pharm. Sci. 64 1975
Molecular Lego¶
A molecule is like a "molecular lego" consisting of the assembly of elementary components (atoms, fragments). Actually there are many commercially available molecular model kits allowing the physical construction of models of small molecules or macromolecules.
articles
New Skeletal-Space-Filling Models Clarke FH J. Chem. Education 54 1977
Plastic Dreiding Models Fieser LF J. Chem. Educations 40 1963
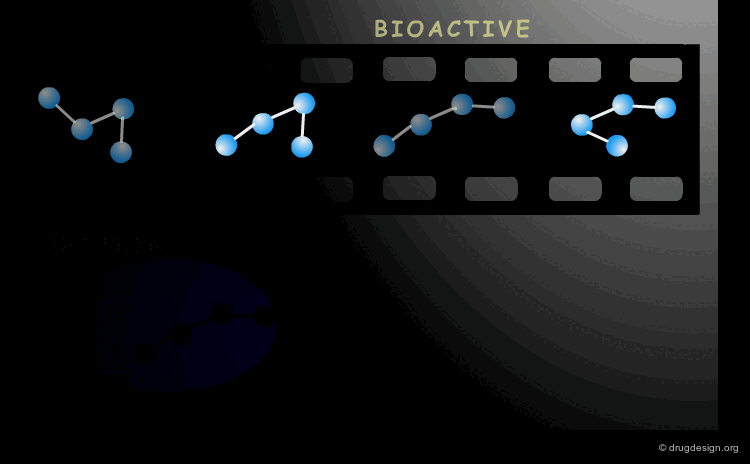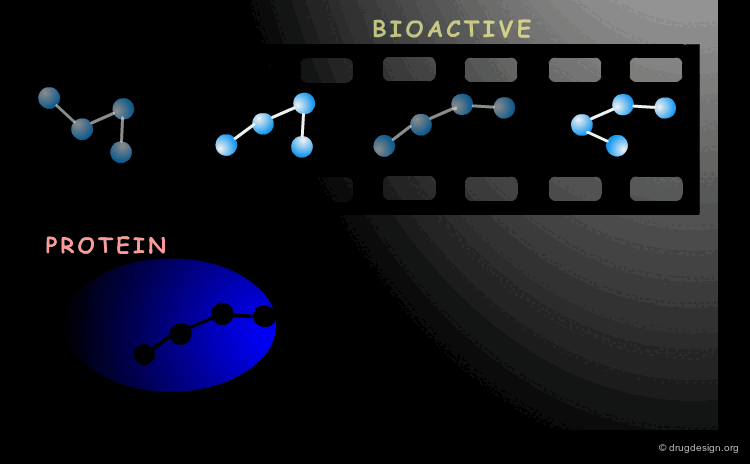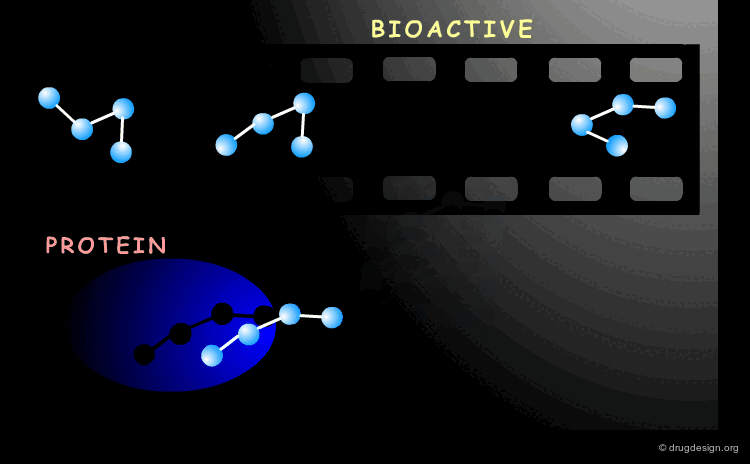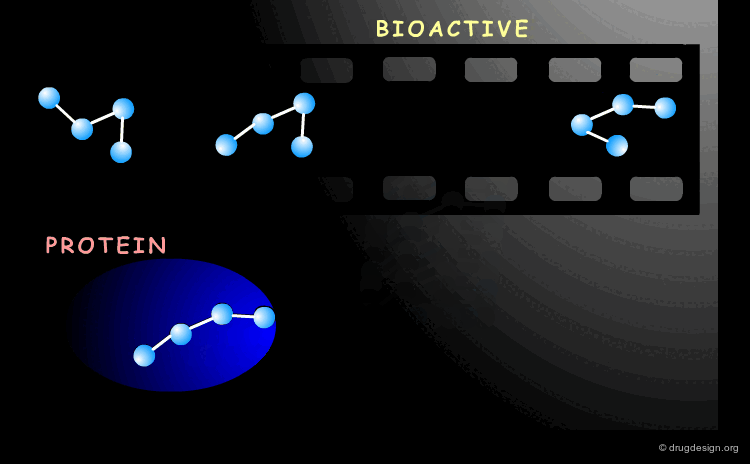
Molecular Fragments for Constructing Molecules¶
This view presents a collection of chemical fragments in their 2D forms along with a static 3D representation of a central molecule
articles
Comparison of Automatic Three-Dimensional Model Builders Using 639 X-ray Structures Sadowski J, Gasteiger J, Klebe G J. Chem. Inf. Comput. Sci. 34 1994
Conformers¶
A Molecule is a Flexible Entity¶
Molecules are far from being static because the atomic forces on atoms create motions and vibrations. Single bonds can be rotated and increase the flexibility of a molecule by altering the relative location of atoms and groups around this bond. Double bonds and rings reduce somewhat the flexibility of a fragment, but not entirely.
Conformation Definition¶
Molecules are dynamic structures and can change their geometries. An individual geometry is called a conformation and a molecule consists of a set of conformers in 3D.
articles
Conformational Energy Calculations on Polypeptides and Proteins Vasquez M, N{eacute}methy G and Scheraga HA Chem. Rev. 94 1994
Example of Conformations of a Molecule¶
The following are example of some of the possible molecular geometries or conformations of a molecule.
Bioactive Conformation¶
A drug interacts with a biological system and the geometry adopted by the molecule when it binds to its biological target it is called the "bioactive conformation". The molecule may have many conformations, however only its bioactive form will trigger the biological process.
articles
Determining the Conformation of a Ligand Bound to an Enzyme Craik DJ, Higgins KA, Kneen MM, Munro SLA and Waterman KJ J. Chem. Ed. 68 1991
A Fast New Approach to Pharmacophore Mapping and its Application to Dopaminergic and Benzodiazepine Agonists Martin YC, Bures MG, Danaher EA, DeLazzer J, Lico I and Pavlik PA J. Comput. Aid. Mol. Des. 7 1993
Applications of Simulated Annealing to Peptides Wilson SR and Cui W Biopolymers 29 1990
Torsion Angles¶
Interconversion Between Conformers¶
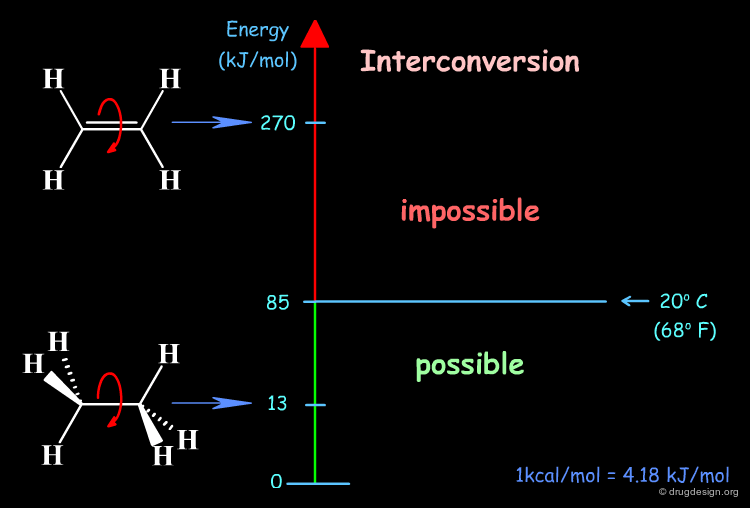
The interconversion between conformations is made by the rotation of single bonds. Interconversion by the rotation of double or triple bonds are not considered, in the first case because of a too high interconversion barrier (in ethylene, 270 kJ/mol), and in the second case the geometry is fixed and the torsion angle has no meaning.
How Do Interconversions Occur?¶
Internal vibrations and thermal motions provide the necessary energy for interconvertion between conformers. However, this is possible only when the torsional barriers are not very high.
articles
The Barrier to Internal Rotation in some Chloro- and Fluoro-Substituted Ethanes Brier PN J. Mol. Structure 6 1970
The Stereochemistry and Interconversion of Nine-membered Rings Containing One Strong Torsional Constraint Glaser R and Shiftan D Advances in Molecular Structure Research 5 1999
Hindered Internal Rotation in Benzophenone Gough KM and Wildman TA J. Am. Chem. Soc. 112 1990
Recognition of Paired Gauche-Gauche Sequences as the Source of the Rotational Barrier in 2,2'-Dimethyl-1,1'-bipiperidines Jaime C and Osawa E J. Chem. Soc. Chem. Comm.
1983
Barriers to Internal Rotation about Single Bonds Lowe JP Prog. Phys. Org. Chem. 6 1968
Definition of the Conformers of a Molecule¶
Molecules change their geometries by rotating single bonds without altering the nature of the atoms and the connectivity (including bond multiplicity), the different geometries are called conformers or conformations.
The Torsion Angle Concept¶
A compound may possess a great number of conformations and an efficient means is needed to describe them. The torsion angle is a useful concept allowing a precise description of the geometry of a molecule. It clearly describes ring and chain conformations as well as interconversion conformational pathways.
articles
The Torsion Angle Concept in Conformational Analysis Bucourt R Topics in Stereochemistry 8 1974
Torsion Angle Coherency in Molecular Orbital Calculations Cohen NC and Kohler B QCPE Bulletin 4 1984
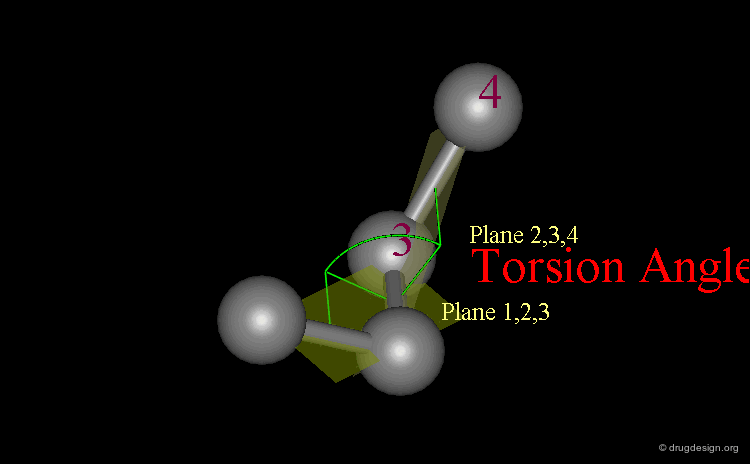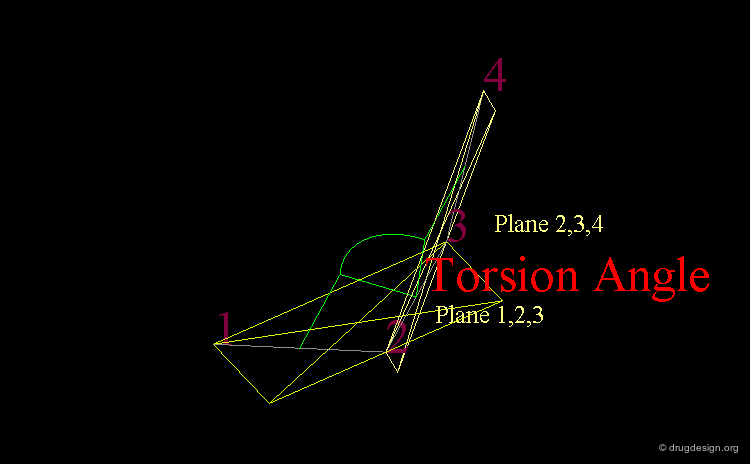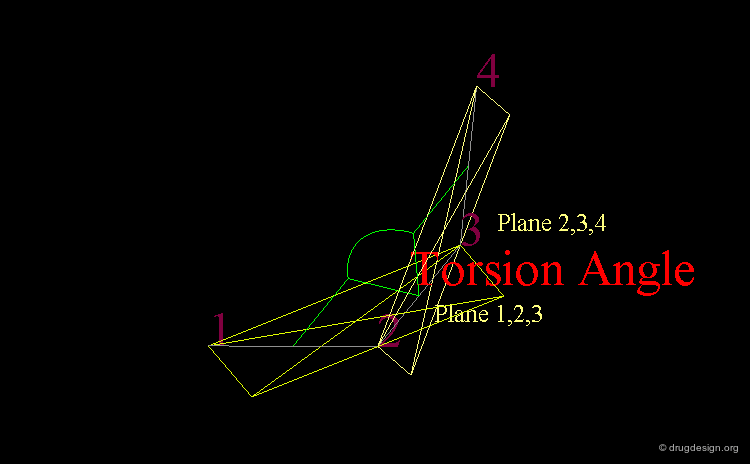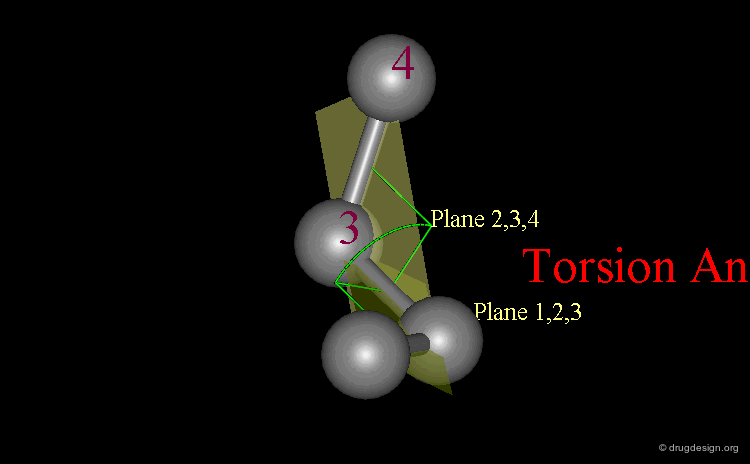
Definition of Torsion Angles¶
A system of three consecutive bonds 1-2, 2-3, 3-4 defines two half-planes (1-2, 2-3) and (2-3, 3-4) intersecting along the central bond 2-3. The torsion angle Φ (1-2-3-4) is the angle between these two half-planes. It gives an accurate description of the relative position of the two vicinal bonds 1-2 and 3-4.
articles
The Torsion Angle Concept in Conformational Analysis Bucourt R Topics in Stereochemistry 8 1974
Torsion Angle Coherency in Molecular Orbital Calculations Cohen NC and Kohler B QCPE Bulletin 4 1984
Monitoring Torsion Angles¶
The geometry of Propanolol changes when the torsion angle of the C(sp3)-C(sp3) central bond is modified. In the following view the value of the angle is zero; the control panel allows this value to be changed interactively. (Clickable picture - click in the purple band to change conformations).
Newman Projections and Torsion Angles¶
The Newman projection is useful for representing the geometry of three consecutive bonds. It is obtained by projecting a plane perpendicular to the central bond. The angle made by the projection of the vicinal bonds in this plane is the torsion angle.
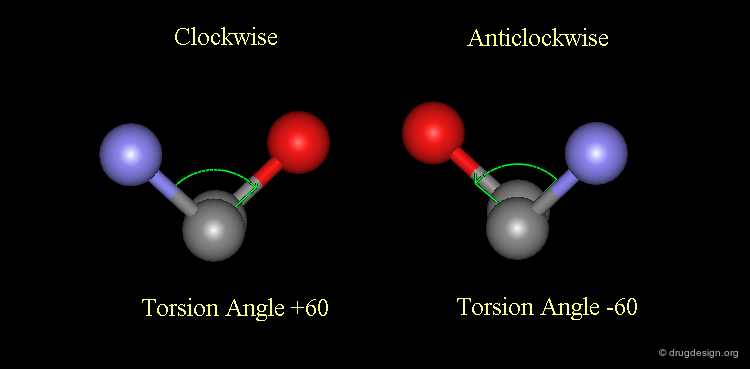
Convention for the Sign of Torsion Angles¶
In the Newman projection for visualizing torsion angles, the torsion angle is positive if the direction of rotation, which superimposes the front bond on the rear bond, is clockwise, and negative if counterclockwise. One should try to avoid absolute values greater than 180°. For example, -120° will be used instead of 240°.
articles
Description of Steric Relationships Across Single Bonds Klyne W and Prelog V Experientia 16 1960
Ring Conformations¶
Whereas torsion angles of acyclic moieties vary independently, this is not true in a ring system. The deformation of any torsion angle of a ring is associated with deformations of the other torsion angles of that ring.
articles
The Stereochemistry and Interconversion of Nine-membered Rings Containing One Strong Torsional Constraint Glaser R and Shiftan D Advances in Molecular Structure Research 5 1999
Molecular Geometry. VII. Modes of Interconversion in the Medium Rings Hendrickson JB J. Am. Chem. Soc 99 1967
The Rate of Chair-Chair Interconversion of Cyclohexane Jensen FR, Noyce DS, Sederholm CH and Berlin AJ J. Am. Chem. Soc. 84 1962
Conformational Complexity¶
Rigid and Flexible Molecules¶
Molecules can be either rigid or flexible, depending on the structural constitution of the molecule.
articles
Comparison of the CHARMM, AMBER and ECEPP Potentials for Peptides. I. Conformational Predictions for the Tandemly Repeated Peptide (Asn-Ala-Asn-Pro)9 Roterman IK, Lambert MH, Gibson KD and Scheraga HA J. Biomol. Struct. Dyn. 7 1989
Conformational Studies of Cyclic Peptide Structures in Solution from 1H-NMR Data by Distance Geometry Calculation and Restrained Energy Minimization Senn H, Loosli HR, Sanner M and Braun W Biopolymers 29 1990
Conformation of β-Hairpins in Protein Structures Sibanda BL, Blundell TL and Thornton JM J.Mol. Biol. 206 1989
book
Blinn JR, Chou KC, Howe WJ, Maggiora GM, Mao B and Moon JB Molecular Aspects of Biotechnology Computational Models and Theories Kluwer Academic Publishers 1992
Codeine and Fenoxedil¶
The more single bonds are present in the structure, the more flexible the molecule is. Ring systems are more rigid entities due to the restricted motions created by the ring.
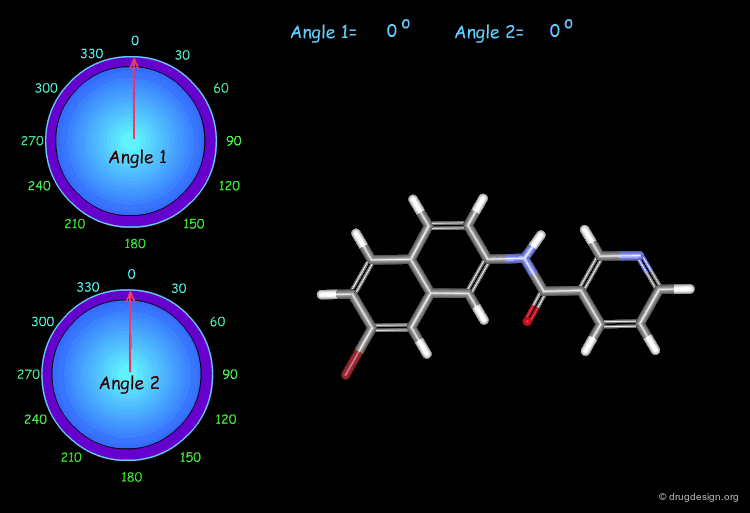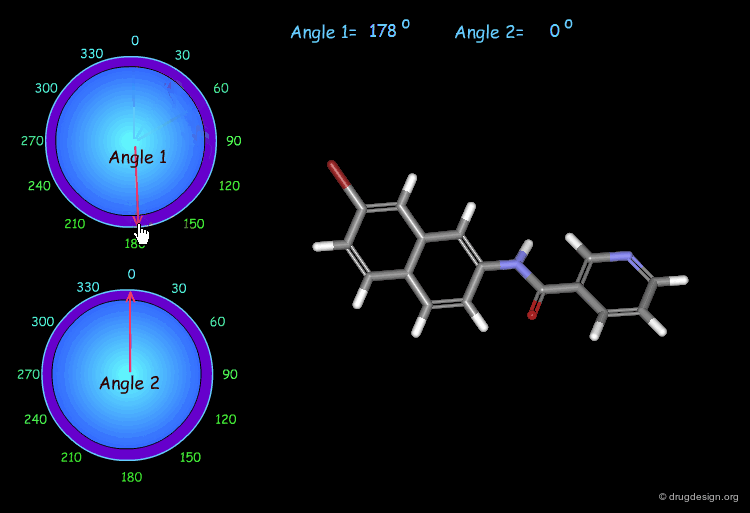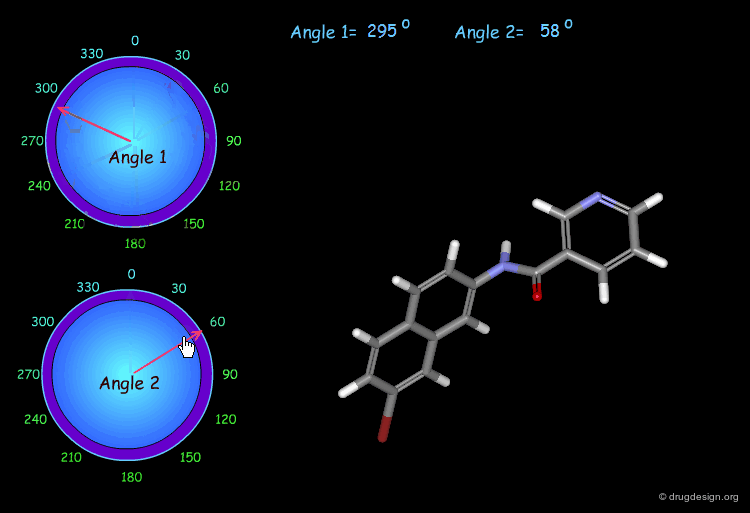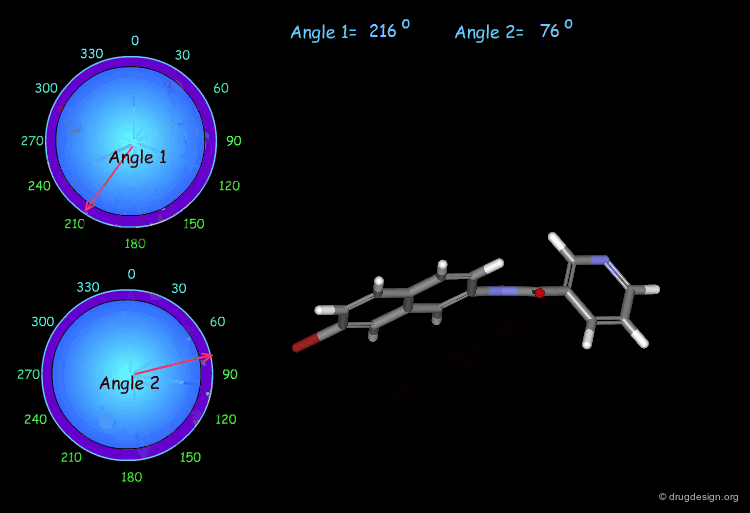
Monitoring Torsion Angle Combinations¶
The molecular geometry of a molecule is a function of the value of its torsion angles. In this example, you can interactively modify two torsion angles (the amide bond cannot rotate) and observe the changes and the modification of the overall molecular shape.
Conformational Explosion¶
Most organic molecules have complex conformations. They may have many single (rotatable) bonds and therefore may exist in a number of conformational states. A typical small organic molecule has 7-8 rotatable bonds and can have several millions of conformations. In the control panels illustrated here, select the number of rotatable bonds and the desired resolution in order to find out how many conformers correspond to your specific input.
articles
Conformational Studies of Cyclic Peptide Structures in Solution from 1H-NMR Data by Distance Geometry Calculation and Restrained Energy Minimization Senn H, Loosli HR, Sanner M and Braun W Biopolymers 29 1990
Ratio of Conformers¶
Mixtures of Conformers¶
A molecule is a mixture of conformers in equilibrium. The "population" of each conformer depends on the energy of each of the individual forms. This is presented in greater detail in the chapters "Molecular Energies" and "Conformational Analysis".
Ratio of Conformers and Population¶
For a molecule consisting of a mixture of conformers, the lower the energy of the conformer, the more it is populated (probability of existence in percent), the total being 100%.
Copyright © 2024 drugdesign.org