Conformational Analysis¶
Info
Conformational analysis is a framework that integrates the information on molecular geometries and energies. Minimization treatments are presented and discussed.
Number of Pages: 54 (±1 hours read)
Last Modified: January 2004
Prerequisites: Molecular Geometry, Molecular Energies
Introduction¶
Geometries, Energies and Conformational Analysis¶
As shown in the previous chapters, a molecule possesses many conformers and an energy is associated to each of these conformations. The aim of this chapter is to present the concept of "conformational analysis" as a framework that integrates the information about geometries and energies discussed in the previous chapters.
Energy Profile: a Global Information¶
The description of the energy of a molecule in the multidimensional space of its degrees of freedom defines the "conformational potential surface" of the compound. This global representation is extremely useful in understanding, assessing, controlling and eventually influencing the properties of a given molecule.
Definition of Conformational Analysis¶
Molecules can change their geometries by processes involving changes in torsion angles. The study of these geometries and their associated energies is called "conformational analysis".
Potential Surface¶
Conformational Potential Surface: One Rotation¶
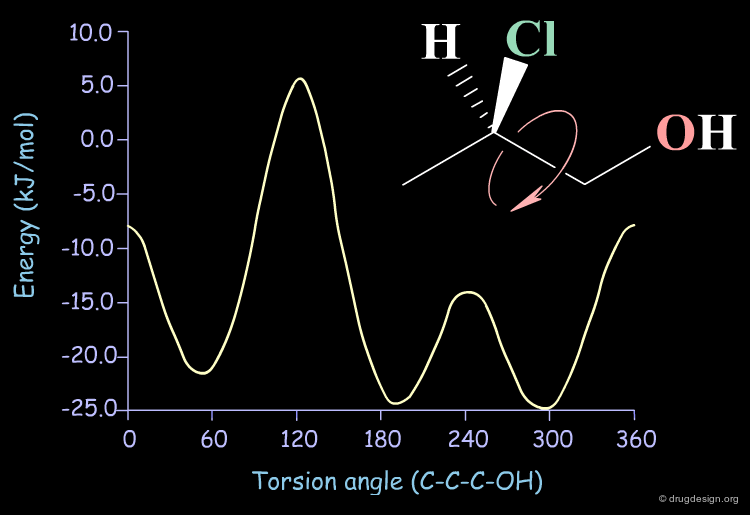
In the case of a molecule with one rotatable bond, the "conformational potential surface" consists of the curve representing the molecular energy as a function of the torsion angle. The minima of the curve correspond to low energy conformations.
articles
Reaction Coordinates and Structure-Energy Relationships Grunwald E Prog. Phys. Org. Chem. 17 1990
Conformational Potential Surface: Two Rotations¶
In the case of a molecule with two rotatable bonds, the total energy is represented (Energy axis) as a function of the two variable torsion angles (Torsion 1 and Torsion 2 axis).
Energy Profile Viewed from the Top¶
This picture represents the same energy profile viewed from the top.
Energy Profile Viewed as Contour Lines¶
The previous representation can also be visualized with contour lines drawn by computers and connecting together all points with the same value of the energy. The energy levels are color-coded.
Conformational Potential Surface¶
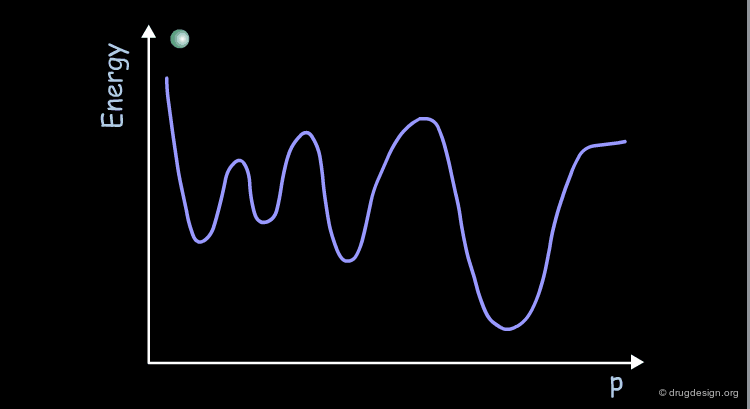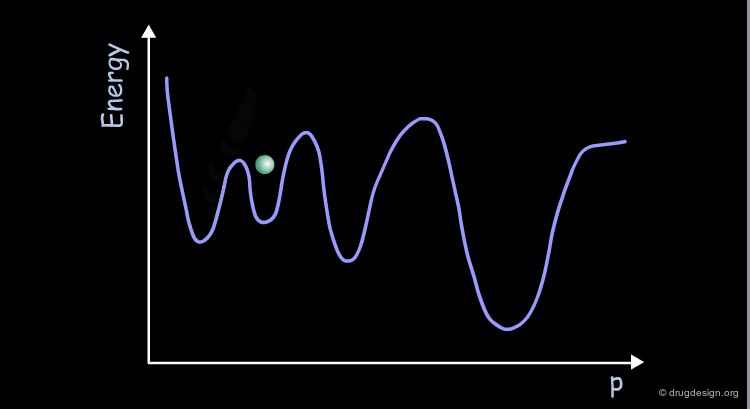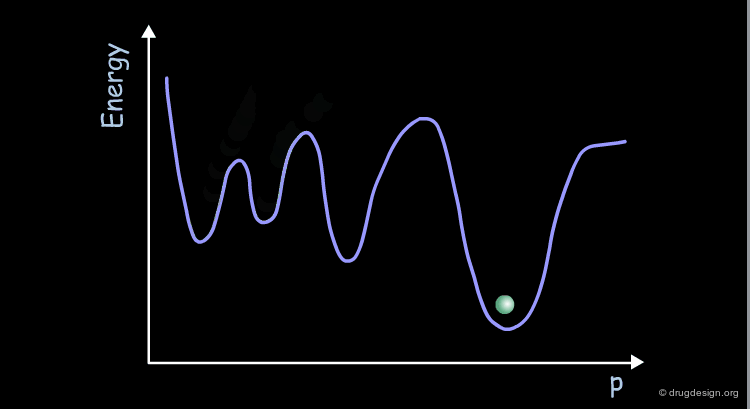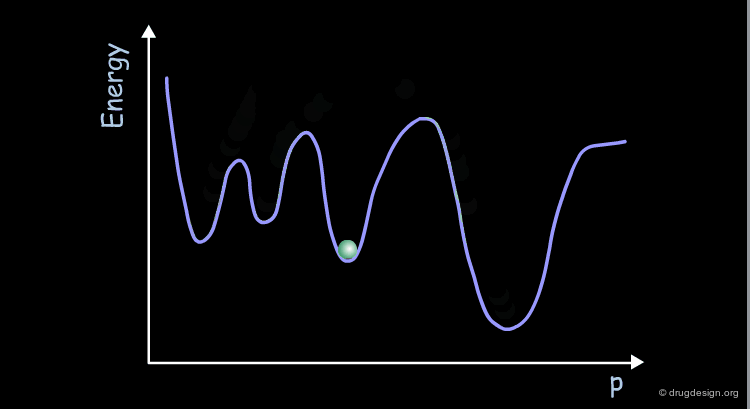
Most molecules have more than two variable torsion angles. Therefore their conformational potential surface cannot be visualized because the surface is defined in a space of more than 3 dimensions. This surface can be represented schematically as a curve displaying the energy as a function of a parameter (p) that has no real geometrical meaning.
articles
An Internal Coordinate Monte Carlo Method for Searching Conformational Space Chang G, Guida WC and Still WC J. Am. Chem. Soc. 111 1989
Automated Conformational Analysis: Directed Conformational Search Using the A* Algorithm Leach AR, Prout K Journal of Computational Chemistry 11 1990
Special Forms¶
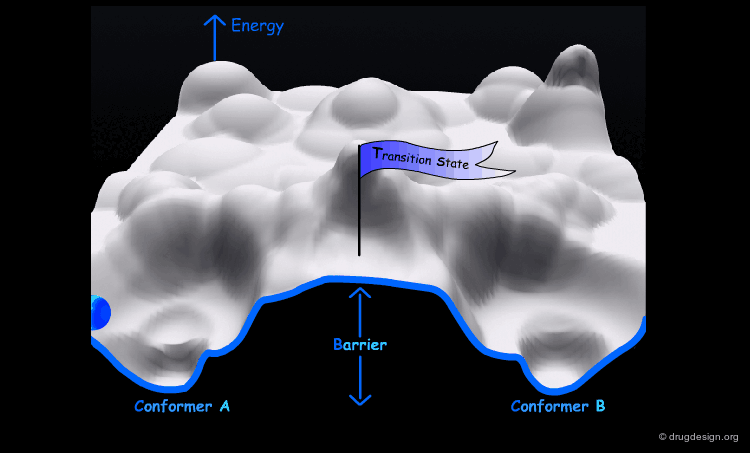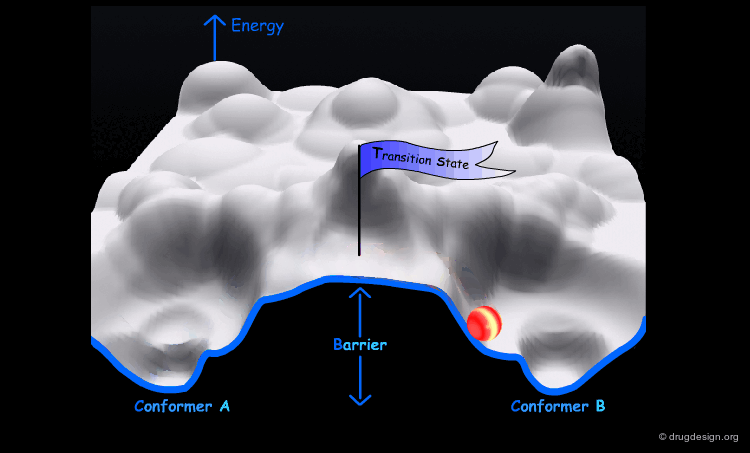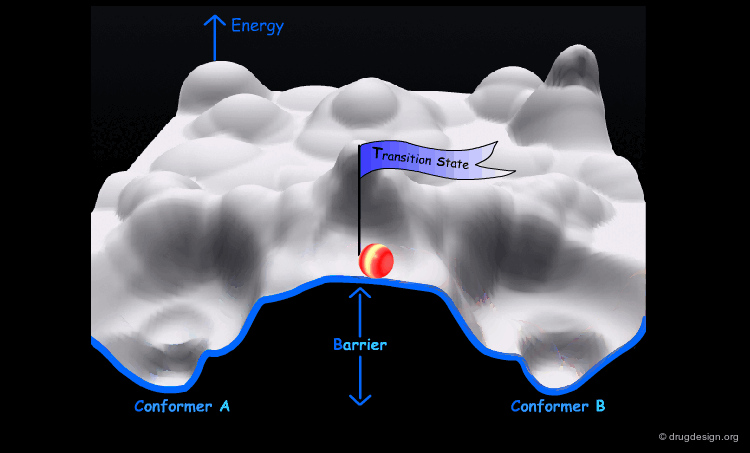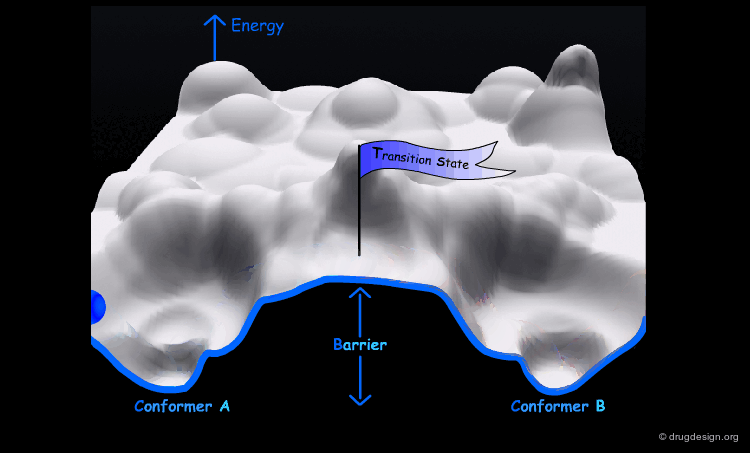
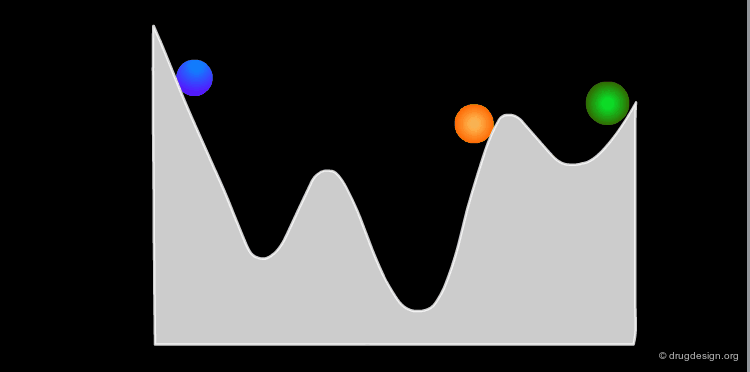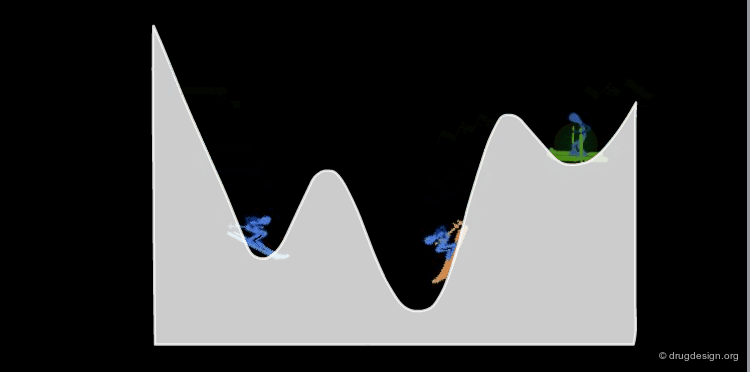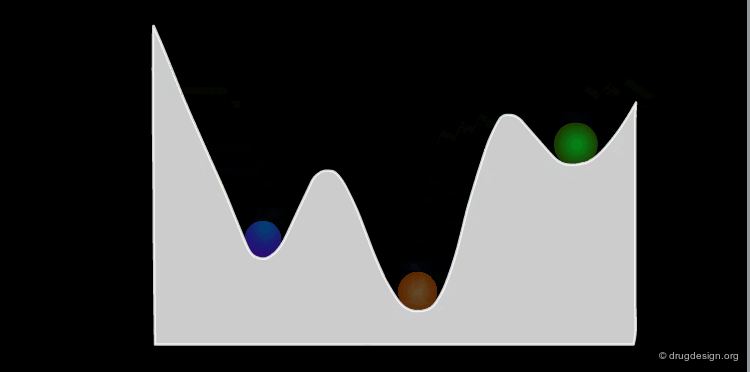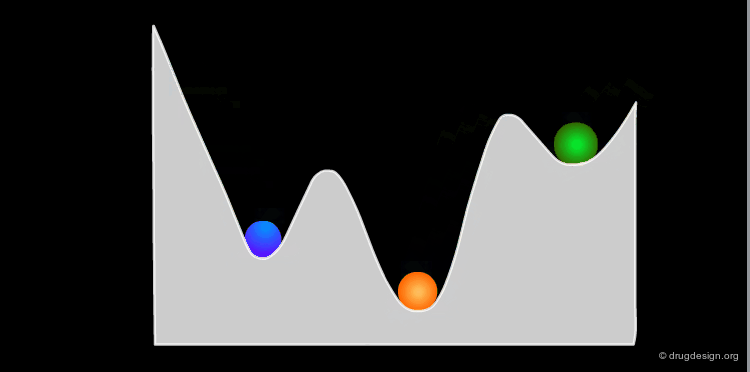
The conformational potential surface contains "local minima" (low energy conformers), "barriers" (high energy conformers), and a "global minimum" (the conformation of lowest energy). Saddle points correspond to points where not all the derivatives of the energy with respect to the coordinates are equal to zero.
Interconversion Between Conformers¶
Conformational minimas are separated by transition states. The interconversion from one conformer to the other requires the crossing of the energy barrier. A low barrier corresponds to rapid interconversion rates. For example for a barrier of about 40 kJ/mol the conversion occurs one million times per second.
articles
Just What is a Transition State? Laidler KJ J. Chem. Education. 65(6) 1988
Energy Barriers¶
When the barrier is high, the interconversion is either slow or impossible. For example for values greater than 80 kJ/mol the interconversion is not possible at room temperature.
articles
Ab Initio Calculation of the Rotational Barriers in Fluorinated Dimethyl Ethers; Solvation Effects on the Rotational Barriers Buono RA, Zauhar RJ and Venanzi CA J. Mol. Struct. (Theochem) 370 1996
Interconversion Pathway¶
The interconversion always proceeds along the pathway of lowest energy. If there is a pathway requiring the crossing of a barrier of less than 80 kJ/mol, it will occur at room temperature.
Conformational Analysis¶
Conformational Analysis Principles¶
The conformational analysis of a molecule results in the full knowledge of its conformational potential surface.
Systematic Scanning of All Potential Surfaces¶
A simple method for exploring the conformational potential surface can be accomplished by a systematic scanning of all geometries of the molecule. Each point of the surface is geometrically constructed and its energy is calculated. This provides comprehensive information about the conformational profile of the molecule.
Systematic Scanning is Time Consuming¶
However the systematic search becomes rapidly impractical. For example, the following molecule has 7 rotatable bonds and one non-planar ring. If we consider a 10° resolution for each rotatable bond (36 conformers per bond) and 4 conformations for the piperazine ring, the numbers of conformers to generate is: 36x36x36x36x36x36x36x4 which correspond to 300 billion conformers. This is unfeasible and impractical.
articles
The Conformational Behavior of n-pentane: A Molecular Mechanics and Molecular Dynamics Experiment Mencarelli P J. Chem. Ed. 72 1995
How to Reduce Conformational Search?¶
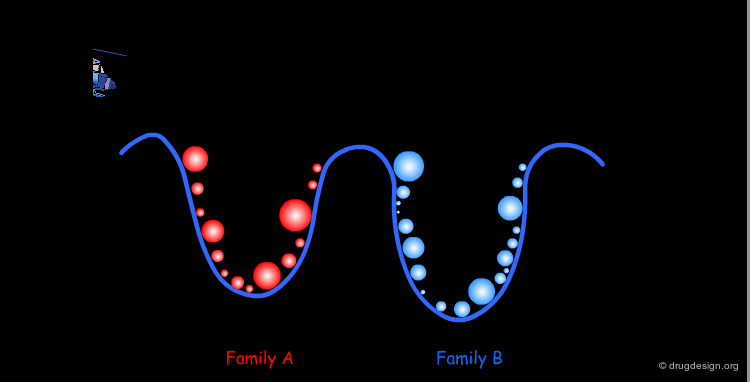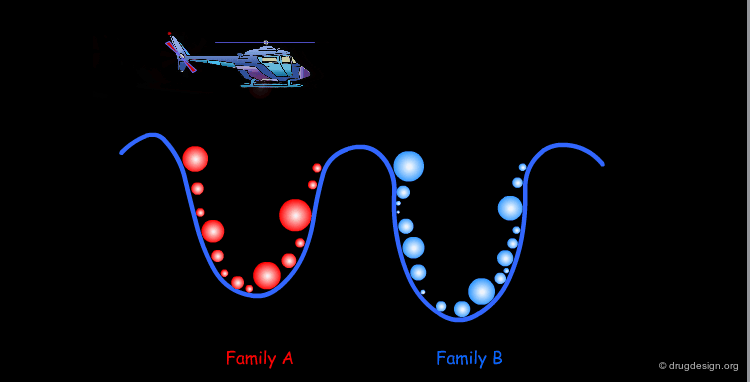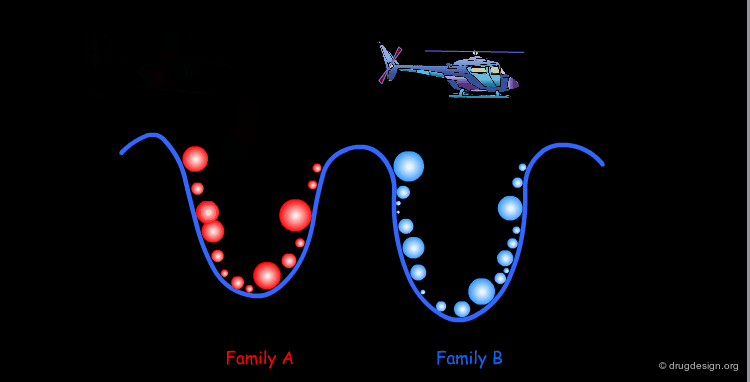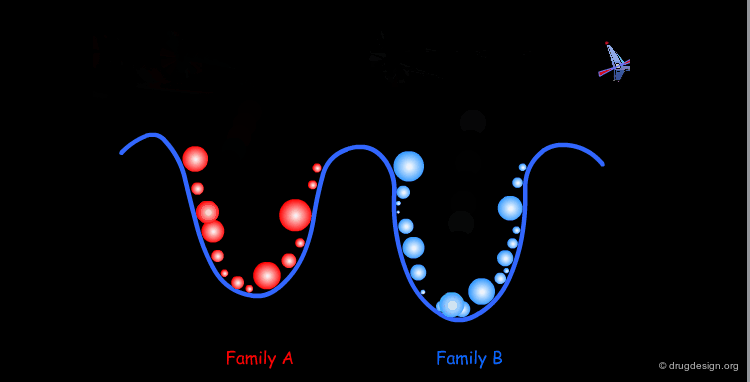
The comprehensive scanning of the surface becomes rapidly impractical; one has to find ways to reduce the number of points. In fact all the geometries inside a given well correspond to a same family of conformers. Therefore, one conformation will be sufficient for representing the entire family. At this point the conformational analysis is reduced to the identification of all the families of conformers for the molecule concerned.
One Conformer Represents a Whole Family¶
The geometrical differences within a given family are in the amplitude and numerical values of the torsion angles; however from the qualitative point of view they are all the same.
articles
Conformations of Peptides and Peptidomimetics by Spectroscopy and Computer Simulation Goodman M, Palmer DE and Said-Nejad OE Polym. Prepr. (Am. Chem. Soc. Div. Polym. Chem.) 31 1990
Conformational Analysis of CCK-B Agonists Using 1H-NMR and Restrained Molecular Dynamics: Comparison of Biologically Active Boc-Trp-(N-Me) Nle-Asp-Phe-NH2 and Inactive Boc-Trp-(N-Me) Phe-Asp-Phe-NH2 Goudreau N, Weng JH, and Roques BP Biopolymers 34 1994
Working with a Set of Representative Conformers¶
With a resolution of 10° the conformers of n-butane will be represented by 36 geometries. However they can be reduced to a much smaller set represented by the local minima. In this case we can select the following three equilibrium geometries: the gauche (+), gauche (-) and the anti, and not 36 positions.
Sildenafil Example¶
With such a rule, all the "typically different" conformers of the molecule are represented. In the example presented here, instead of studying hundred billions of forms, we now have only to study 8748 (3x3x3x3x3x3x3x4=8748) conformers.
Family Representatives: Small Rings¶
Select a given ring size and select the bond multiplicity scheme you want for the ring (i.e. single or double bonds). The conformations associated to the system you have chosen appear both in 2D (with the signs of the torsion angles) and in 3D.
Family Representatives: Acyclic Bonds¶
Describe the nature of the central bond atoms and their hybridization. Newman representations appear and are clickable.
Consequence: Minimization Treatments¶
In drug design applications, the minima and their relative energies are of central importance. The representative forms that are generated correspond to theoretical forms and they are not necessarily at the minimum of their corresponding well. Their energies are meaningless. In order to have meaningful values, one has to relax their geometries to find the point of minimum energy; this treatment is called "minimization".
Example: Analysis of Elementary Fragments¶
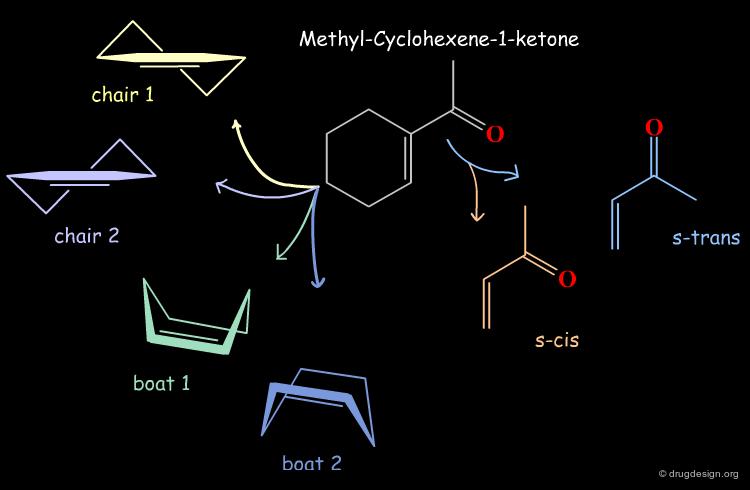
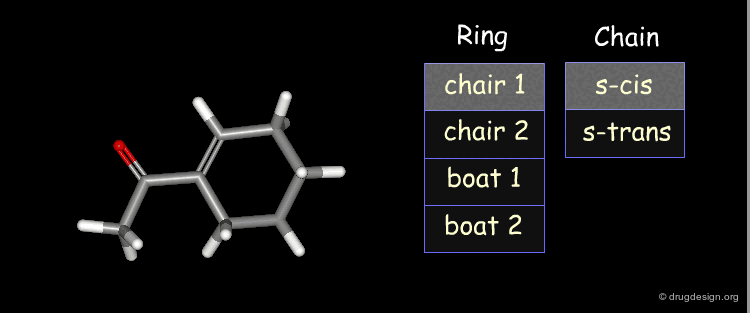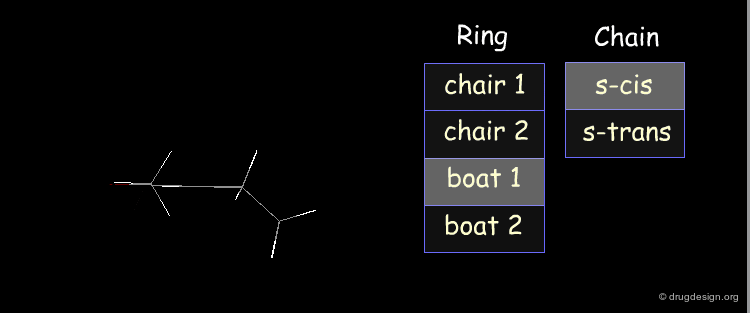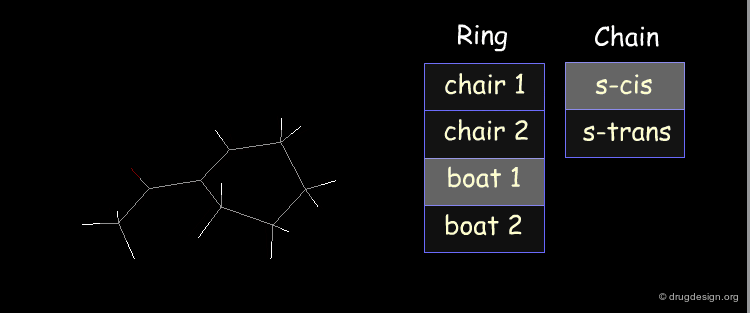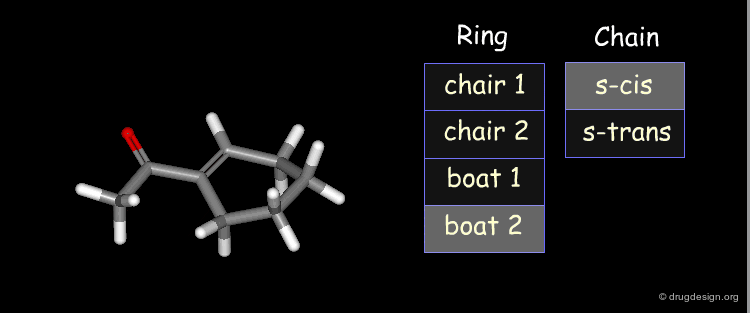
Let us visualize the analysis of methyl-cyclohexene-1-ketone. The carbonyl of the keto group can be either s-trans or s-cis relative to the double bond of the ring. The cyclohexene ring can adopt 4 different conformations (2 chairs and 2 boats).
Example: Generation of Representative Conformers¶
The representative geometries of the molecule can be represented by a set of 2x4 = 8 typically different conformers.
Example: Results of Conformational Analysis¶
The forms were all minimized and the following relative energies were obtained:
Conformational Analysis Principles: Summary¶
In the great majority of molecules, it is not possible to systematically generate all their conformers. One has to consider a method that produces typically different conformers. They can be generated either by the analysis of their fragments or by random methods (e.g. Monte Carlo). Minimizations procedures then have to be considered for meaningful energy values.
Minimizations¶
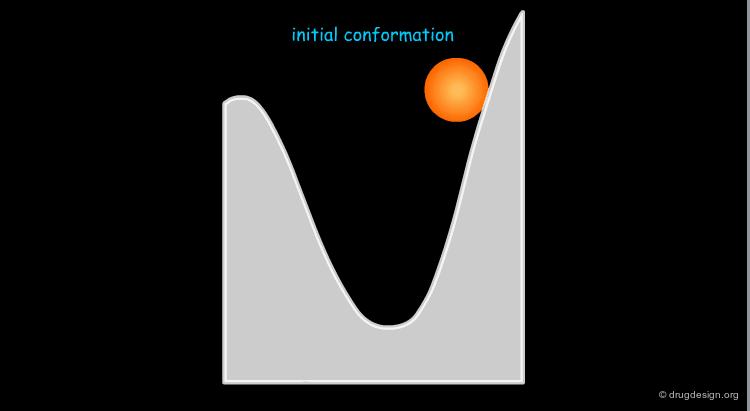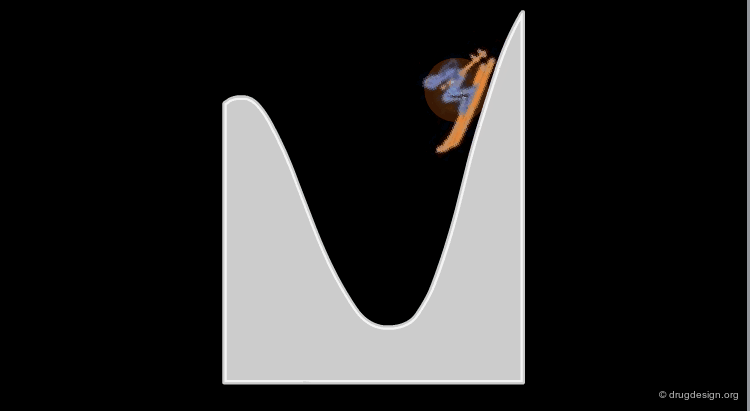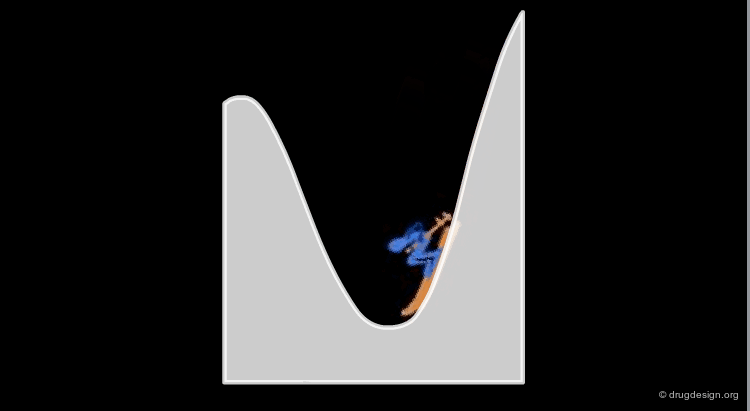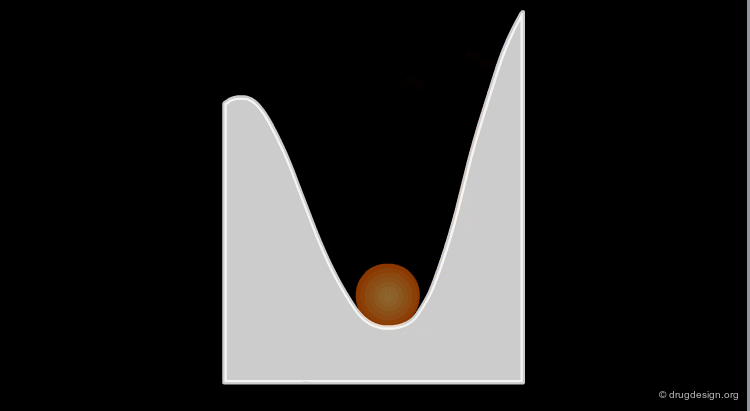
Definition of the Minimization of a Conformer¶
Minimization treatment consists of successive alterations of the geometry of the molecule until a minimum is found on the conformational potential surface. The minimization is terminated when it is not possible to find a conformer of lower energy in the current well considered.
Improved Geometries and Good Energies¶
A non-minimized conformer may be used for rough geometrical analyses but not for energy considerations. A minimized structure is a good model for both the geometry and the energy.
The Minimization Treatment¶
In energy minimization an initial conformation is submitted to full geometry optimization, where all parameters defining the geometry of the system are modified by small increments, until the total energy of the system reaches a minimum.
How Does Minimization Works?¶
Small modifications of the molecular geometry are considered, if the resulting geometry has a lower energy than the original, then another step is made in the same direction. Otherwise a smaller step in a different direction is carried out. The process is continued until the energy cannot decrease.
articles
Global Energy Minimization by Rotational Energy Embedding Crippen GM and Havel TF J. Chem. Inf. Comput. Sci. 30 1990
book
Polak E Optimization: Algorithms and Consistent Approximations Springer 1997
Minimization Methods¶
There are different algorithms for conducting a minimization. For example, for the steepest descent, the conjugated gradients or Newton-Raphson procedures require the calculation of the first or second derivatives of the energy all along the iterative process.
articles
Quasi-Newton Methods and their Application to Function Minimization Broyden CG Math. Comput. 21 1967
A Rapidly Convergent Descent Method for Minimization Fletcher R and Powell MJD Comput. J. 6 1963
Function Minimization by Conjugate Gradients Fletcher R and Reeves CM Comput. J. 7 1964
A Broyden-Fletcher-Goldfarb-Shanno Optimization Procedure for Molecular Geometries Head JD and Zerner MC Chem. Phys. Lett. 122 1985
Simplex Method for Function Minimization Nelder JA and Mead R Comput. J. 7 1965
An Efficient Method for Finding the Minimum of a Function of Several Variables without Calculating Derivatives Powell MJD Comput. J. 7 1964
Many Variables Are Minimized¶
Bond lengths, bond angles and torsion angles are the variables of the minimization process. The total energy of the following molecule is a function of 132 variables.
Minimization is a Time-Consuming Treatment¶
The minimization of one conformer may require thousands of iterations, each one requiring the calculation of the new energy. Moreover the minimization treatment has to be applied thousands of times (one minimization for each conformer generated).
Examples of Minimization¶
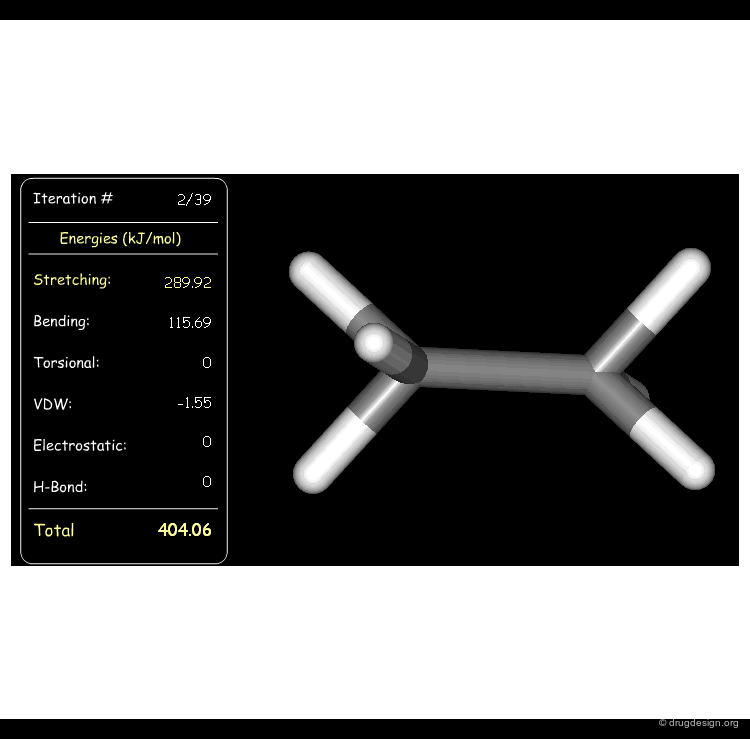
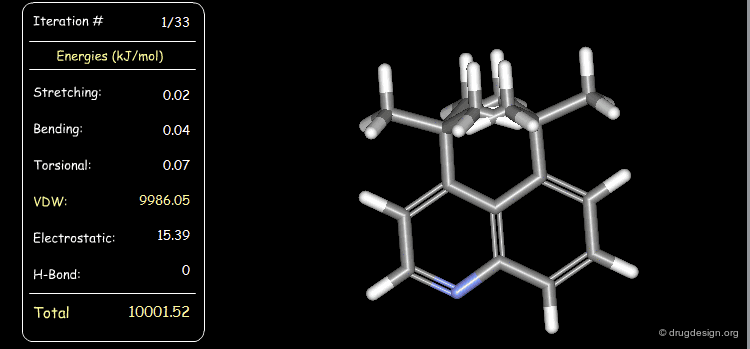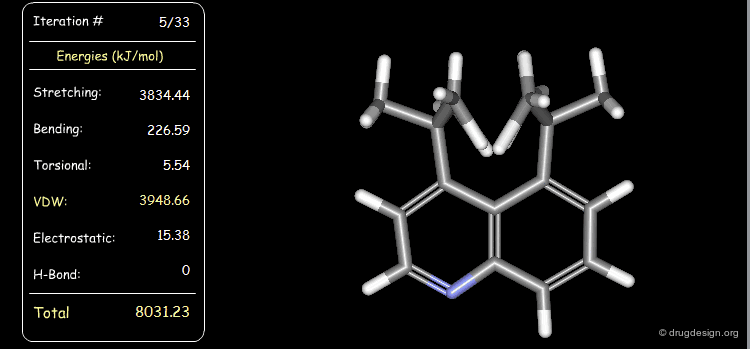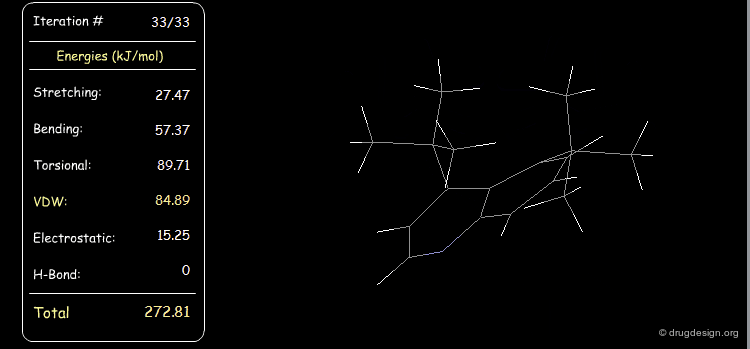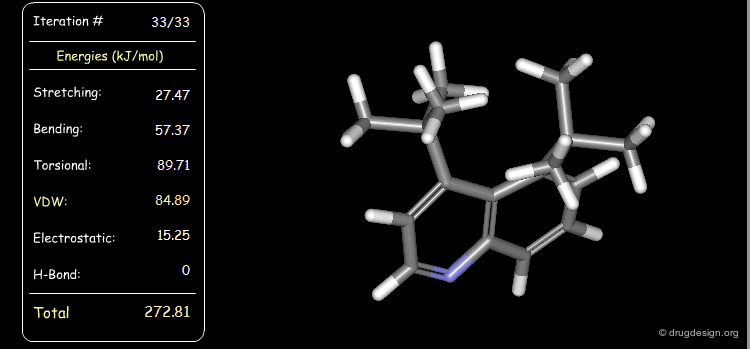
Minimization with Stretching Strain¶
The stretching energy of the starting geometry is extremely high. Press the START button to initiate the minimization process and note the variation of each of the elementary contributions (e.g. stretching, bending, van der Waals) until the lowest energy conformation is reached.
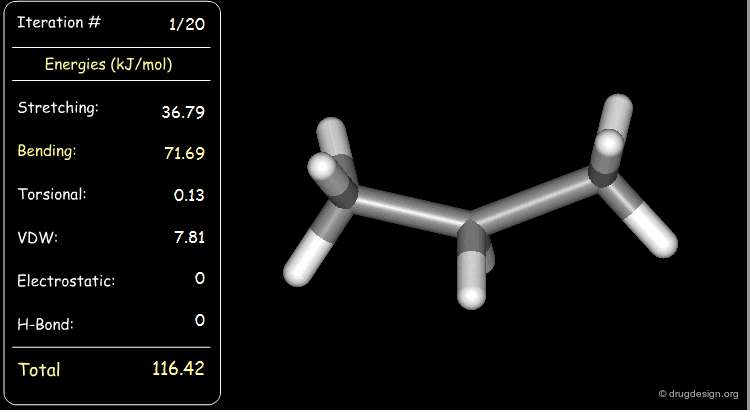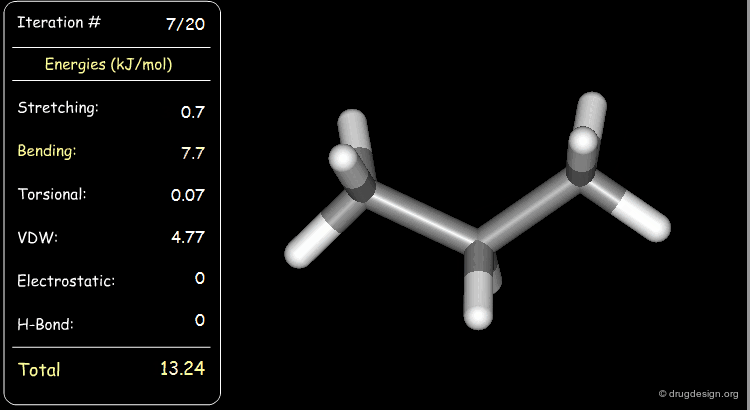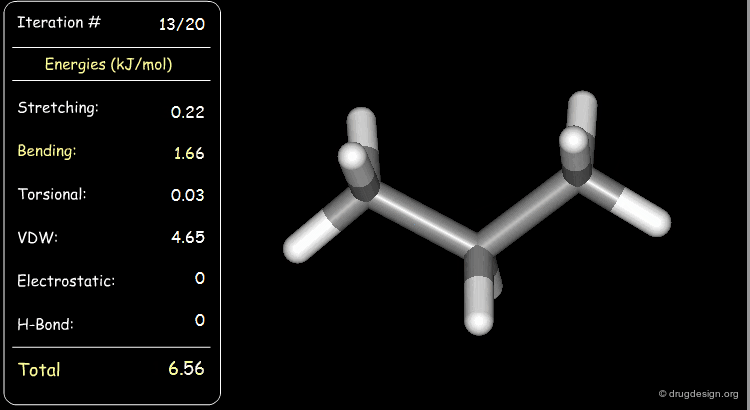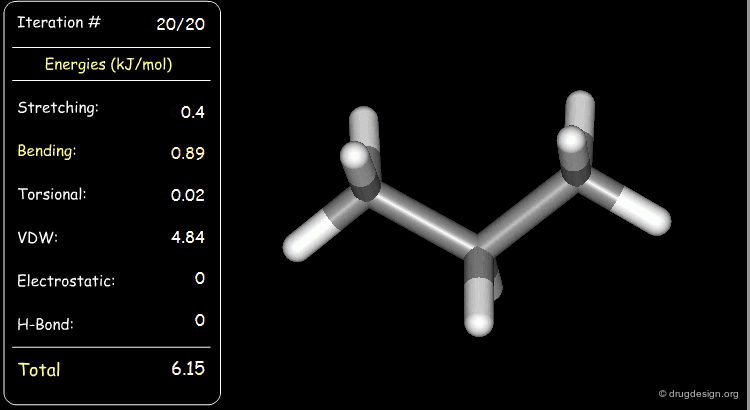
Minimization with Bending Strain¶
Stretching, bending, and van der Waals energies of the starting geometry are high. Press the START button to initiate the minimization process and note their variation until the lowest energy conformation is reached.
Minimization with Torsional Strain¶
Torsional and van der Waals energies of the starting geometry are high. Press the START button to initiate the minimization process and note their variation until the lowest energy conformation is reached.
Minimization with Van der Waals Strain¶
In their initial relative orientations the van der Waals interactions between the two molecules are not optimal. Press the START button to view how the minimization of the entire system achieves better interactions with shorter distances and finally finds the minimum energy.
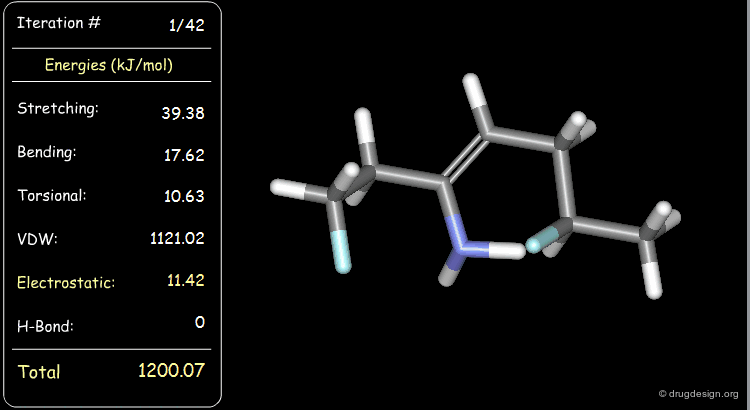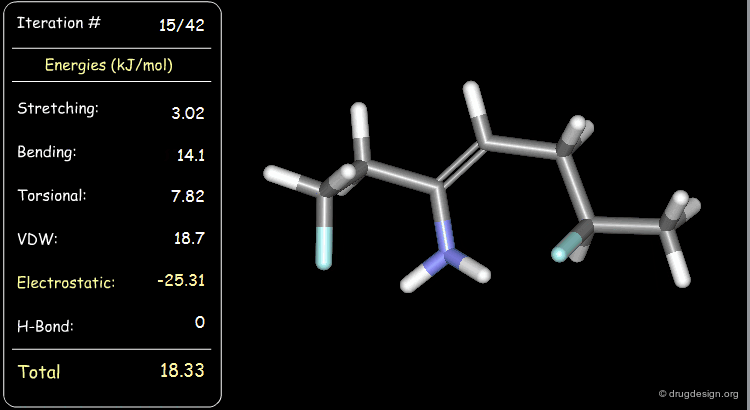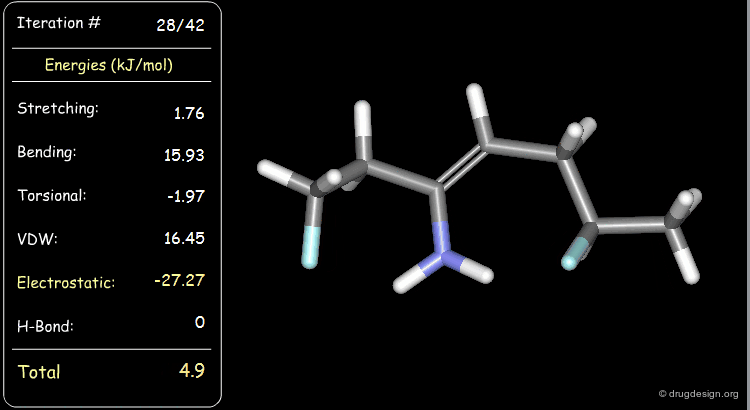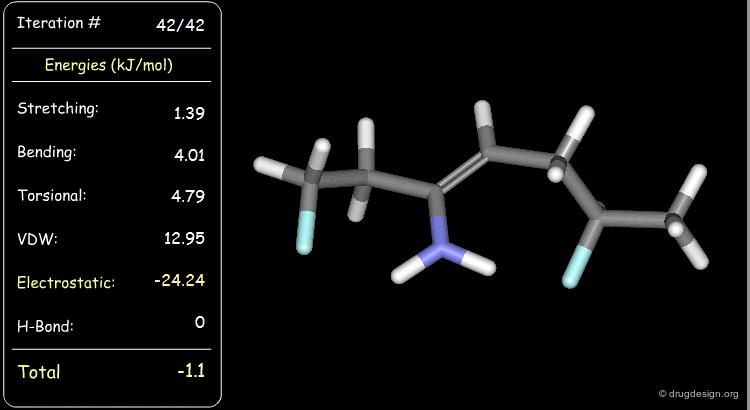
Minimization with Electrostatic Component¶
The electrostatic component of the starting conformer is small and at the end of the minimization, it turns negative (attractions).
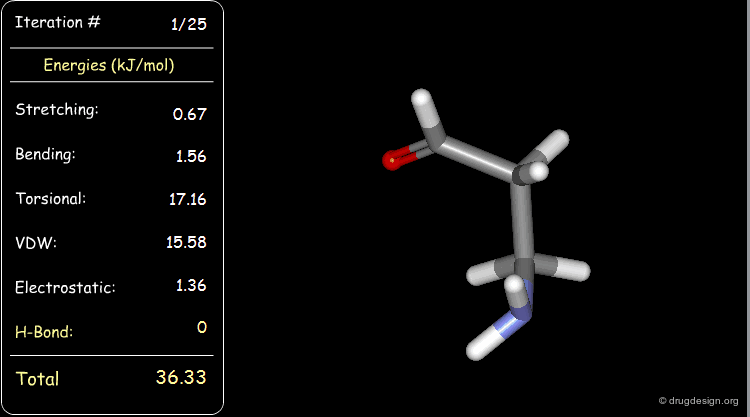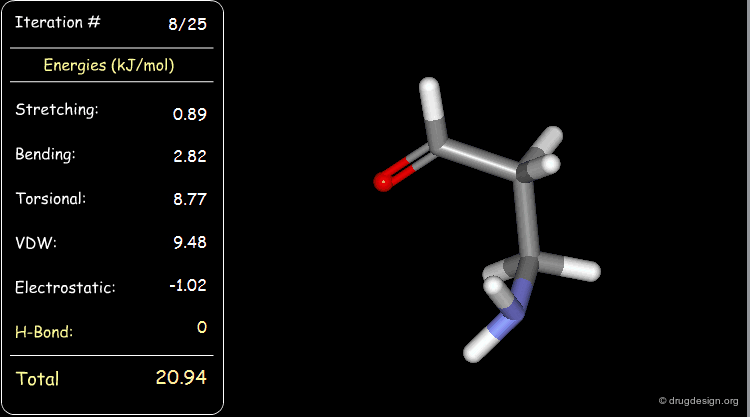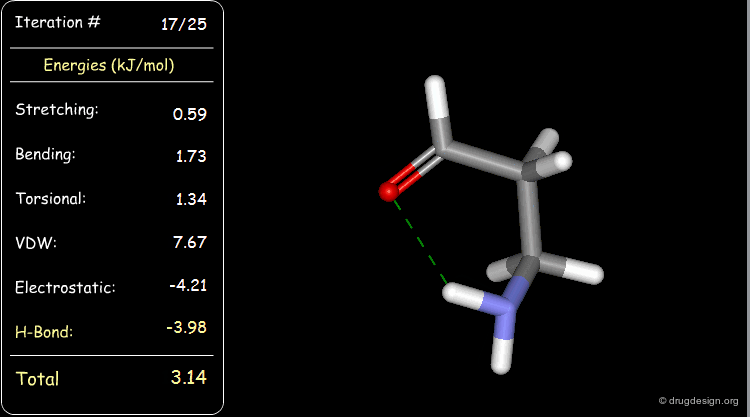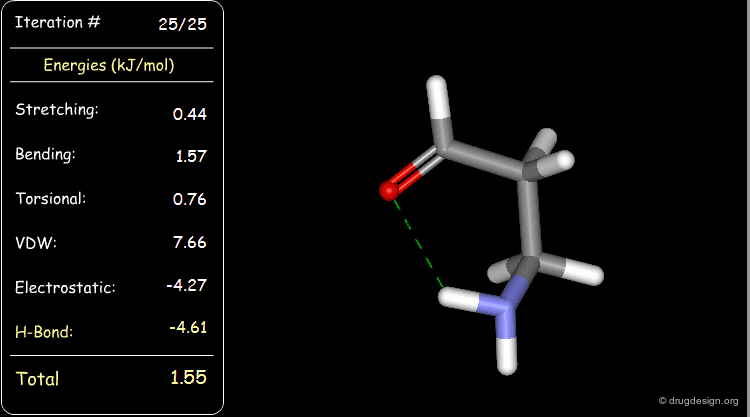
Minimization with Hydrogen Bond Component¶
Press the START button to view how the minimization process optimizes a favorable intramolecular hydrogen bond.
Distribution of Energy Strain¶
The following example illustrates a case where the strain energy of the starting conformer is high due to severe van der Waals repulsions and can be reduced only with substantial deformations of other components including torsional, stretching and bending energies. In the final minimized conformer, the forces acting on the atoms are all balanced.
Conformational Analysis in Drug Design¶
Conformational Analysis in Drug Design¶
Conformational analysis and drug design are two independent disciplines. They have in common the conformation (and energy) of the bioactive form. Conformational analyses are used to predict the biological properties of candidate prototype structures.
Energy of the Bioactive Form¶
In order to be able to assess the population of the bioactive form, it is necessary to know the energy of the global minimum of the molecule concerned. This requires conformational analysis studies.
Low Energy of the Bioactive Conformation¶
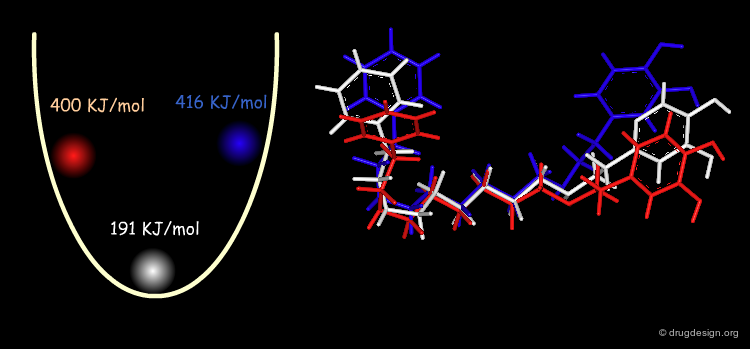
The difference of energy between the bioactive conformation and the conformation found in the crystal is generally less than 13 kJ/mol; this can be understood in the framework of the "induced-fit" theory.
articles
Conformation of Acetylcholine Bound to the Nicotinic Acetylcholine Receptor Behling RW, Yamane T, Navon G and Jelinski LW Proc. Natl. Acad. Sci. USA 85 1988
Geometry of the Bioactive Conformation¶
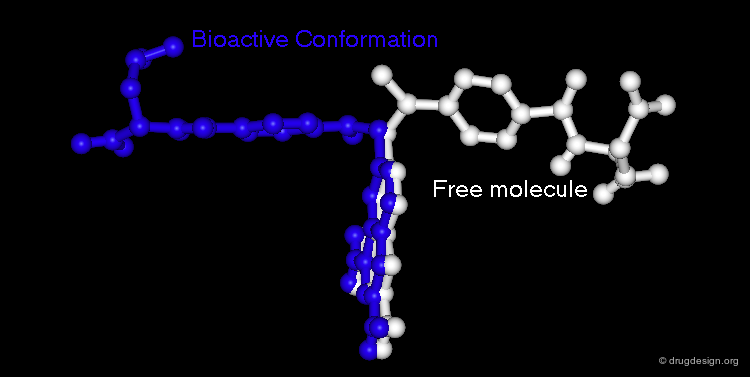
The geometry of the bioactive conformation of a molecule can be very different from the conformation of the isolated molecule in solution or in the crystal, let alone the isolated (in vacuo) state given by energy minimization. The example shown here illustrates the case of methotrexate where the conformation of the free molecule is shown in white, and in blue when the molecule is bound to its biological target.
articles
Conformation of Acetylcholine Bound to the Nicotinic Acetylcholine Receptor Behling RW, Yamane T, Navon G and Jelinski LW Proc. Natl. Acad. Sci. USA 85 1988
Search Strategies for Determining Bioactive Conformers of Peptides and Small Molecules Burt SK and Greer J Annual Reports in Medicinal Chemistry 23 1988
The Experienced Molecular Modeler¶
A good molecular modeler can intelligently save time-consuming treatments. He can judge, assess, and estimate using the 3D manipulation of a mechanical molecular model until he feels that a calculation is needed. For example, an experienced modeler can easily guess the geometry of the global minimum of a molecule and possibly minimize 5-10 different candidate geometries instead of the thousands that would be needed in a fully computerized study. He will use the computerized treatments for clarifying features that are beyond the things he knows.
articles
Conformational Differences Between alfa-Cyclodextrin in Aqueous Solution and in Crystalline Form Koehler JEH, Sanger W and van Gunsteren WF J. Mol. Biol. 203 1988
Common Errors Made with Minimization¶
Among the common errors that are observed in the use of molecular modeling systems is the belief that a minimized conformer has a "quality label" of validity. This is not true. The minimum obtained depends on the initial conformation that has been used. Although 'improved' by the minimization treatment, this is not sufficient. What is important is the location of this conformation with respect to the low energy minima, including the global minimum of the molecule.
articles
Abuses of Molecular Mechanics. Pitfalls to Avoid Lipkowitz BK J. Chem. Educ. 72 1995
Example 1¶
This is an example of a minimized molecule corresponding to an input conformation introduced by the modeler. The problem is that the "cis" conformation of an acyclic ester is almost inexistent; the "trans" form is by far the preferred one. The population of this conformation visualized here is close to 0%. The same can also be said for amide bonds.
Example 2¶
The following is a representation of a minimized conformation of a molecule where two bulky groups are in a 1-3 diaxial orientation. The molecule will not stay in this conformation. The cyclohexane ring will change its conformation and adopt the alternative chair conformer in which the two substituents will be both in an equatorial orientation. The population of the conformation visualized here is close to 0%.
Molecular Dynamics¶
Molecular Dynamics¶
Molecular dynamics provide an alternative approach to determine the preferred conformers and the global minimum of a molecule. This is achieved by the simulation of the dynamical motions of the molecule as it vibrates and undergoes internal rotation.
Theoretical Basis of Molecular Dynamic Calculations¶
Molecular dynamics is an extension of the molecular mechanics approach and based on the idea that the atoms of the molecule feel forces and want to move. Each atom is treated as a particle responding to Newton's equations of motion. Integration of these equations with successive time steps lead to the trajectory of the atoms over time in the form of a list of positions and velocities.
articles
Molecular dynamics simulations: A tool for drug design Rognan D Perspect. Drug Discov. Des. 9 1998
Local Minima and Global Minimum¶
Molecular dynamic simulations can be used to obtain low energy conformers. The simulations can run with differing temperatures to obtain different families of conformers. At higher temperatures, more conformers are possible and it becomes feasible to cross energy barriers. Current methodology and computer capabilities do not allow the sampling of the conformational space of large molecules.
articles
The Multiple Minima Problem in the Conformational Analysis of Molecules. Deformation of the Potential Energy Hypersurface by the Diffusion Equation Method Piela L, Kostrowicki J and Scheraga HA J. Phys. Chem. 93 1989
Some Approaches to the Multiple-Minima Problem in the Calculation of Polypeptide and Protein Structure Scheraga HA Int. J. Quantum Chem. 42 1992
Simulated Annealing, a Special Type of Dynamics¶
Simulated annealing is a technique where the molecule is heated and then cooled very slowly so that conformational changes occurring will be at a local minimum. This process is generally repeated many times until several very closely related and low energy conformations are obtained. The conformer of lowest energy is assumed to be global minimum.
Coherency of Molecular Motions¶
The motions of the atoms and chemical groups obtained by molecular dynamics simulation reveal subtle underlying molecular machinery. In the beginning of the simulation, the motions are frequently interrupted by collisions with neighboring groups and each group seems to have an erratic trajectory. However, over longer periods of time, coherent and collective motions start to develop, revealing how some groups can fluctuate somewhat more than others.
A Typical Molecular Dynamics Run¶
Typically one can generate about 100 conformations and minimize them with molecular mechanics. The minimized forms are used as starting points for dynamics simulation varying the time and temperature. For each starting point, a number of steps of dynamics at 1 femtosecond intervals are made; the coordinates and energy of each point are recorded. The conformation representing every picosecond steps is saved, and finally, at the end of the study, the atoms' trajectories can be displayed as a movie by quickly displaying the sequence of individual frames. Throughout the treatments, conformers with low energies are saved (coordinates and energies).
Copyright © 2024 drugdesign.org